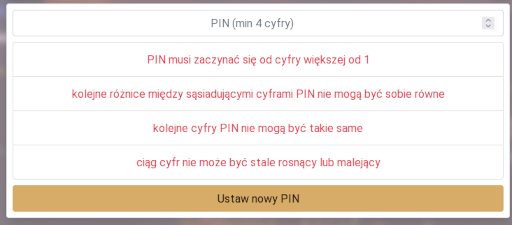
Będzie o PINach, a ogólniej o hasłach, bo PIN to specyficzny rodzaj hasła. Less is more to w tym przypadku mniej ograniczeń przekładających się na większe bezpieczeństwo. Zaczęło się od wpisu na Twitterze gdzie pokazano ograniczenia nakładane na PIN w pewnej aplikacji.
Zastanowiło mnie, czy da się policzyć o ile takie ograniczenia zmniejszą bezpieczeństwo, rozumiane jako przestrzeń możliwych poprawnych kombinacji PINu.
Na wstępie widać, że pierwsza cyfra PINu musi być inna niż 0 oraz 1. Już sam ten warunek zmniejsza przestrzeń poprawnych PINów o 20%. I to niezależnie od długości PINu.
Tu moja matematyka wysiada i sięgam po symulacje. Skrypt w Pythonie, który sprawdza wszystkie czterocyfrowe kombinacje i podaje, czy PIN jest poprawny (True) czy błędny (False) może wyglądać tak:
def is_valid(a, b, c, d):
if a < 2:
return False
if ((a - b) == (b - c) or (b - c) == (c - d)):
return False
if (a == b) or (b == c) or (c == d):
return False
if ((b - a > 0) and (c - b > 0) and ((d - c > 0)) or (b - a < 0) and (c - b < 0) and (d - c < 0)):
return False
return True
for a1 in range(0, 10):
for a2 in range(0, 10):
for a3 in range(0, 10):
for a4 in range(0, 10):
result = is_valid(a1, a2, a3, a4)
print(a1, a2, a3, a4, result)
python piny.py | grep -c True
5120
Jak widać, dla PINów o czterech cyfrach, wprowadzone ograniczenia zmniejszają przestrzeń dozwolonych PINów aż o niemal połowę.
Po co te ograniczenia i jak to zrobić poprawnie?
I teraz o motywacji. Jestem pewnien, że była ona szczytna i chodziło o podniesienie bezpieczeństwa. Jestem prawie pewien, że twórcy chodziło o wyeliminowanie prostych, schematycznych PINów. 0000, 1111, 1234 itp. Jak widać, w praktyce konsekwencje były dalej idące.
Najlepiej biorąc pod uwagę statystyki najczęściej występujących PINów i tworząc krótką listę PINów zabronionych. Wg statystyk PIN 1234 odpowiada za ponad 10% wystąpień wśród używanych PINów. 20 najczęściej używanych PINów jest używanych w 26% przypadków. Taka lista podniesie bezpieczeństwo, rozumiane jako „wymuszenie mało popularnego PINu” równie skutecznie, co proponowane ograniczenia. Zaś bezpieczeństwo rozumiane jako „ilość możliwych kombinacji” zostanie zmniejszone jedynie minimalnie.
Przypadki brzegowe
Jeśli przypuszczamy, że nasi klienci mają znacząco różne preferencje niż te z powyższych statystyk, robi się trudniej. W ogólności najlepiej walidować hasła na obecność zabronionych ciągów już w momencie ustalania hasła przez użytkownika. Zabronić można nazwy firmy, zasobu do którego jest chroniony dostęp, roku, czy popularnych ciągów znaków.
Jeśli jednak tego nie zrobiliśmy zawczasu, nadal nie wszystko stracone, choć robi się nieco ślisko. Nie znamy przecież PINów, co najwyżej mamy dostęp do hashy, więc ciężko będzie określić, których używają nasi klienci. Na ratunek przychodzi hashcat. Niezależnie od użytej funkcji hashującej, brute force krótkich PINów trwa moment. Jeśli korzystamy z bezpiecznych, wolno liczonych hashy, a użytkowników jest wielu, nie ma potrzeby robienia brute force wszystkich. Wystarczy analiza próbki statystycznej. Oczywiście taki audyt to operacja bardzo delikatna, więc nie zabieramy się za to bez stosownych umocowań i zachowania właściwej higieny.
UPDATE: Wersja uogólniona skryptu poniżej. Ilość cyfr w PIN regulowana ilością powtórzeń alfabetu w funkcji product. Dla dłuższych PINów warto skorzystać z pypy, które potrafi być szybsze.
import itertools
alphabet = list(range(0, 10))
def is_valid(i):
if i[0] < 2:
return False
for n in range(0, len(i)-2):
if i[n] - i[n+1] == i[n+1] - i[n+2]:
return False
for n in range(0, len(i)-1):
if i[n] == i[n+1]:
return False
monotonic = True
for n in range(0, len(i)-2):
if (i[n] - i[n+1]) * (i[n+1] - i[n+2]) < 0:
return True
if monotonic:
return False
return True
for i in itertools.product(alphabet, alphabet, alphabet, alphabet):
result = is_valid(i)
print(i, result)